 |
| Fig. 1 Intensity plot of C/2011 L4 (March 3 2013). Numbers indicate intensity levels in greyscale (0 - black ; 255 - white) |
On last March 3rd I took some photos of C/2011 L4 (Panstars). Here I present an excercise of astrometry using one of those images to extract some meaningful data from this observation. What I do here can be applied to any other comet image or, in fact, celestial object in the sky. My aim is to show a simple example of practical applicaton of mathematics and geometry in the determination of sizes of celestial objects.
My interest is:
For that aim, we need:
- To estimate the apparent (in minutes of arc) and real dimension of the tail (in km or mi) of C/2011 L4;
- To estimate the apparente (in minutes of arc) and real dimension of the coma (in km or mi);
For that aim, we need:
- Comet image with date;
- Scale calibration;
- Software to extract brightness levels (the so called 'isointensity' curves);
- Distance of Earth to the comet at the date;
- Comet position angle in relation to the sun at the date;
I should also mention the need of a good sky simulator software (for all practical purposes I will use Stellarium, but other software could work as well). These are the 'inputs' of the work and the 'outputs' are described above, the physical dimension of the comet (at least an approximate value for this dimension).
Below I coment step-by-step all procedures that I used to find the final estimates. This exercise demonstrates a practical aspect of astronomical observation, something that is fully in agreement with the objectives of this blog.
Below I coment step-by-step all procedures that I used to find the final estimates. This exercise demonstrates a practical aspect of astronomical observation, something that is fully in agreement with the objectives of this blog.
1) Comet image with date
I use the image publish on last March 4 2013 reproduced below. The image was acquired on March 3rd at 22:15 UT and it is an important input for the determination of additional parameters as we will see.
 |
| Fig. 2 Image used for the exercise. (click on the image to enlarge) |
2) Scale calibration
Fig.2 shows not only Panstarrs but also a star named HIP 117488 of mag. 7.0. This star was easily identified with Stellarium using the date and time as input for the skymap display. The apparente distance between the star image centroid and the 'comet nucleus' is about 40' (forty minutes of arc) - Fig. 3.
Then we calculate the distance in pixels on the image between HIP 117488 and the comet and find 355.1. Therefore the scale factor (Sf) will be
Sf = 40'/355.1 ~ 0.113'/pixel.
This is nearly 6" per pixel and corresponds to the final resolution of the image. Note that this value is the overall resolution of both the combined optics and camera setup.
The resolution above is a practical scale for the determination of the comet dimension. Using Stellarium, we find that at the observation date, the comet-Earth (observer) distance (D) was:
D=1.09843629 AU.
Since 1 AU = 149,597,870,700 meters (92,955,807.273 mi) and Sf in radians is
Sf(rad) = 0.000032763 rad/pixel
then
Sf(km)= Sf(rad)*D(km) = 5383.74 km/pixel (=3345.3 mi/km)
Therefore, each pixel in the image at the comet position corresponds to about 5400 km. The smallest pixel in the image, in particular the one corresponding to the "comet nucleus", is a square of ~5400 x 5400 km, much larger than the expected physical size of that nucleus.
3) Detail analysis of the cometary image
The image is in fact a matrix of intensities on an arbitrary scale (in a grey scale 8 bit image, the intensity goes from 0 to 255). If we extract a small portion of the original image (after converting it to grey scale), say, a square of 35X35 centered at HIP 117488, we get Fig. 4.
A 3D intensity plot of this image is shown in Fig. 5. This plot was made with Mathcad. What about the cometary image? I resampled the original image to 310 X 460 after converting it to greyscale and the resulting 3D intensity plot is:
The intensity of the coma region is close to 255 (the maximum) and should be compared to the 'background' level between 10 and 15. Another possibility is to ask Mathcad to plot the intensity curves (Fig. 1). The tail length in pixels as estimated using Fig. 1 is about 90.5. Therefore the (aparent) tail length is
 |
| Fig. 3 Estimate of apparent distance between HIP 117488 and comet C/2011 L4 at the date as given by Stellarium. |
Sf = 40'/355.1 ~ 0.113'/pixel.
This is nearly 6" per pixel and corresponds to the final resolution of the image. Note that this value is the overall resolution of both the combined optics and camera setup.
The resolution above is a practical scale for the determination of the comet dimension. Using Stellarium, we find that at the observation date, the comet-Earth (observer) distance (D) was:
D=1.09843629 AU.
Since 1 AU = 149,597,870,700 meters (92,955,807.273 mi) and Sf in radians is
Sf(rad) = 0.000032763 rad/pixel
then
Sf(km)= Sf(rad)*D(km) = 5383.74 km/pixel (=3345.3 mi/km)
Therefore, each pixel in the image at the comet position corresponds to about 5400 km. The smallest pixel in the image, in particular the one corresponding to the "comet nucleus", is a square of ~5400 x 5400 km, much larger than the expected physical size of that nucleus.
3) Detail analysis of the cometary image
The image is in fact a matrix of intensities on an arbitrary scale (in a grey scale 8 bit image, the intensity goes from 0 to 255). If we extract a small portion of the original image (after converting it to grey scale), say, a square of 35X35 centered at HIP 117488, we get Fig. 4.
 |
| Fig. 4 A small sample of the original image showing HIP 117488. |
 |
| Fig. 5 Intensity surface of Fig. 3 of HIP 117488. |
 |
| Fig. 6 3D intensity plot of the original image showing the comet and HIP 117488. |
- Apparent Tail(km) = 90.5 x Sf(km) ~ 490 000 km (= ~ 300 000 mi)
- Apparent Tail(min of arc) = 10.2'
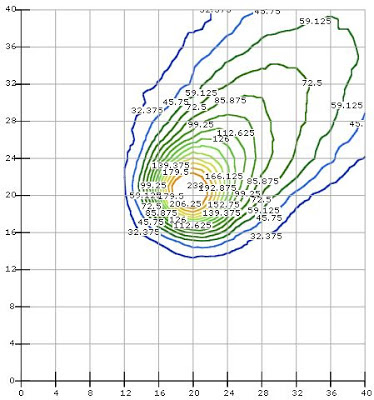 |
| Fig. 7 Intensity plot of the coma. |
A minor detail
It could be argued (with reason) that the estimated tail size must be corrected for the geometrical situation shown in Fig.8. The comet tail always points towards the sun (along the Sun-comet line), while we are observing the projection of this line on the perpendicular to the Earth-comet line.
 |
| Fig. 8 |
Real Tail(km) = Apparent Tail(km)/cos(alpha).
Now, again using Stellarium we have:
Des = 0.99156172 AU;
phi = 18 deg 40' (elongation angle);
as the Earth-Sun distance and elongation angle for comet Panstarrs at the date, respectively. Therefore, using the above equation we find:
alpha = 26 deg 33',
so that cos (alpha) = 0.8944249989.
The real tail length in km (mi) will be
Real Tail(km) = 90.5 x Sf(km)/cos(alpha) = 545 000 km (~340 000 mi).
Compare this with the Earth-Moon distance (384 400km). There is no accurate definition of a comet tail (that depends on the density of particles such as dust, gas etc). What we can say here, however, is that, given the "definition" of tail as determined by the smallest intensity level on Fig. 1 (30.5), the real tail extended itself for half a million kilometers in space on the date.
References
- Stellarium - a free open source planetarium for your computer;
- PTC Mathcad - The Industry Standard for Engineering Calculations;
- JPL Small-Body Database Browser: C/2011 L4 (PANSTARRS;


Nenhum comentário:
Postar um comentário